Runs the Compound Poisson-Gamma chronology model of Haslett and Parnell (2008)
Source:R/Bchronology.R
Bchronology.RdFits a non-parametric chronology model to age/position data according to the Compound Poisson-Gamma model defined by Haslett and Parnell (2008) <DOI:10.1111/j.1467-9876.2008.00623.x>. This version uses a slightly modified Markov chain Monte Carlo fitting algorithm which aims to converge quicker and requires fewer iterations. It also a slightly modified procedure for identifying outliers
Bchronology(
ages,
ageSds,
positions,
positionThicknesses = rep(0, length(ages)),
calCurves = rep("intcal20", length(ages)),
ids = NULL,
outlierProbs = rep(0.01, length(ages)),
predictPositions = seq(min(positions), max(positions), length = 100),
pathToCalCurves = system.file("data", package = "Bchron"),
artificialThickness = 0.01,
allowOutside = FALSE,
iterations = 10000,
burn = 2000,
thin = 8,
extractDate = 1950 - as.numeric(format(Sys.time(), "%Y")),
maxExtrap = 1000,
thetaStart = NULL,
thetaMhSd = 0.5,
muMhSd = 0.1,
psiMhSd = 0.1,
ageScaleVal = 1000,
positionEps = 1e-05,
positionNormalise = TRUE
)Arguments
- ages
A vector of ages provided in years before 1950.
- ageSds
A vector of 1-sigma values for the ages given above
- positions
Position values (e.g. depths) for each age. In the case of layers of non-zero thickness, this should be the middle value of the slice
- positionThicknesses
Thickness values for each of the positions. The thickness value should be the full thickness value of the slice. By default set to zero.
- calCurves
A vector of values containing either
intcal20,shcal20,marine20, ornormal(older calibration curves are supposed such as intcal13). Should be the same length the number of ages supplied. Non-standard calibration curves can be used provided they are supplied in the same format as those previously mentioned and are placed in the same directory. Normal indicates a normally-distributed (non-14C) age.- ids
ID names for each age
- outlierProbs
A vector of prior outlier probabilities, one for each age. Defaults to 0.01
- predictPositions
A vector of positions (e.g. depths) at which predicted age values are required. Defaults to a sequence of length 100 from the top position to the bottom position
- pathToCalCurves
File path to where the calibration curves are located. Defaults to the system directory where the 3 standard calibration curves are stored.
- artificialThickness
Amount to add to the thickness values in the case of equal positions with no
positionThicknesses. Bchron may fail ifpositionThicknessesare zero and some positions are repeated. This value is added on to the zero thicknesses (only in the case of repeated positions) to stop this failure.- allowOutside
Whether to allow calibrations to run outside the range of the calibration curve. By default this is turned off as calibrations outside of the range of the calibration curve can cause severe issues with probability ranges of calibrated dates
- iterations
The number of iterations to run the procedure for
- burn
The number of starting iterations to discard
- thin
The step size for every iteration to keep beyond the burn-in
- extractDate
The top age of the core. Used for extrapolation purposes so that no extrapolated ages go beyond the top age of the core. Defaults to the current year
- maxExtrap
The maximum number of extrapolations to perform before giving up and setting the predicted ages to NA. Useful for when large amounts of extrapolation are required, i.e. some of the
predictPositionsare a long way from the dated positions- thetaStart
A set of starting values for the calendar ages estimated by Bchron. If NULL uses a function to estimate the ages. These should be in the same units as the posterior ages required. See example below for usage.
- thetaMhSd
The Metropolis-Hastings standard deviation for the age parameters
- muMhSd
The Metropolis-Hastings standard deviation for the Compound Poisson-Gamma mean
- psiMhSd
The Metropolis-Hastings standard deviation for the Compound Poisson-Gamma scale
- ageScaleVal
A scale value for the ages.
Bchronologyworks best when the ages are scaled to be approximately between 0 and 100. The default value is thus 1000 for ages given in years.- positionEps
A small value used to check whether simulated positions are far enough apart to avoid numerical underflow errors. If errors occur in model runs (e.g.
missing value where TRUE/FALSE neededincrease this value)- positionNormalise
Whether to normalise the position values.
Bchronologyworks best when the positions are normalised to be between 0 and 1 The default value isTRUE
Value
A list of class BchronologyRun which include elements:
- theta
The posterior estimated values of the ages
- phi
The posterior estimated outlier values (1=outlier, 2=not outlier). The means of this parameter give the posterior estimated outlier probabilities
- mu
The posterior values of the Compound Poisson-Gamma mean
- psi
The posterior values of the Compound Poisson-Gamma scale
- thetaPredict
The posterior estimated ages for each of the values in predictPosition
- predictPositions
The positions at which estimated ages were required
- calAges
The calibrated ages as output from
BchronCalibrate- inputVals
All of the input values to the
Bchronologyrun
Details
The Bchronology function fits a compound Poisson-Gamma distribution to the increments between the dated levels. This involves a stochastic linear interpolation step where the age gaps are Gamma distributed, and the position gaps are Exponential. Radiocarbon and non-radiocarbon dates (including outliers) are updated within the function also by MCMC.
References
Haslett, J., and Parnell, A. C. (2008). A simple monotone process with application to radiocarbon-dated depth chronologies. Journal of the Royal Statistical Society, Series C, 57, 399-418. DOI:10.1111/j.1467-9876.2008.00623.x Parnell, A. C., Haslett, J., Allen, J. R. M., Buck, C. E., and Huntley, B. (2008). A flexible approach to assessing synchroneity of past events using Bayesian reconstructions of sedimentation history. Quaternary Science Reviews, 27(19-20), 1872-1885. DOI:10.1016/j.quascirev.2008.07.009
See also
Examples
# \donttest{
# Data from Glendalough
data(Glendalough)
# Run in Bchronology - all but first age uses intcal20
GlenOut <- with(
Glendalough,
Bchronology(
ages = ages,
ageSds = ageSds,
calCurves = calCurves,
positions = position,
positionThicknesses = thickness,
ids = id,
predictPositions = seq(0, 1500, by = 10)
)
)
#> Running Bchronology...
#>
|
| | 0%
|
| | 1%
|
|= | 1%
|
|= | 2%
|
|== | 3%
|
|== | 4%
|
|=== | 4%
|
|=== | 5%
|
|=== | 6%
|
|==== | 6%
|
|==== | 7%
|
|===== | 8%
|
|===== | 9%
|
|====== | 9%
|
|====== | 10%
|
|====== | 11%
|
|======= | 11%
|
|======= | 12%
|
|======== | 13%
|
|======== | 14%
|
|========= | 14%
|
|========= | 15%
|
|========= | 16%
|
|========== | 16%
|
|========== | 17%
|
|=========== | 18%
|
|=========== | 19%
|
|============ | 19%
|
|============ | 20%
|
|============ | 21%
|
|============= | 21%
|
|============= | 22%
|
|============== | 23%
|
|============== | 24%
|
|=============== | 24%
|
|=============== | 25%
|
|=============== | 26%
|
|================ | 26%
|
|================ | 27%
|
|================= | 28%
|
|================= | 29%
|
|================== | 29%
|
|================== | 30%
|
|================== | 31%
|
|=================== | 31%
|
|=================== | 32%
|
|==================== | 33%
|
|==================== | 34%
|
|===================== | 34%
|
|===================== | 35%
|
|===================== | 36%
|
|====================== | 36%
|
|====================== | 37%
|
|======================= | 38%
|
|======================= | 39%
|
|======================== | 39%
|
|======================== | 40%
|
|======================== | 41%
|
|========================= | 41%
|
|========================= | 42%
|
|========================== | 43%
|
|========================== | 44%
|
|=========================== | 44%
|
|=========================== | 45%
|
|=========================== | 46%
|
|============================ | 46%
|
|============================ | 47%
|
|============================= | 48%
|
|============================= | 49%
|
|============================== | 49%
|
|============================== | 50%
|
|============================== | 51%
|
|=============================== | 51%
|
|=============================== | 52%
|
|================================ | 53%
|
|================================ | 54%
|
|================================= | 54%
|
|================================= | 55%
|
|================================= | 56%
|
|================================== | 56%
|
|================================== | 57%
|
|=================================== | 58%
|
|=================================== | 59%
|
|==================================== | 59%
|
|==================================== | 60%
|
|==================================== | 61%
|
|===================================== | 61%
|
|===================================== | 62%
|
|====================================== | 63%
|
|====================================== | 64%
|
|======================================= | 64%
|
|======================================= | 65%
|
|======================================= | 66%
|
|======================================== | 66%
|
|======================================== | 67%
|
|========================================= | 68%
|
|========================================= | 69%
|
|========================================== | 69%
|
|========================================== | 70%
|
|========================================== | 71%
|
|=========================================== | 71%
|
|=========================================== | 72%
|
|============================================ | 73%
|
|============================================ | 74%
|
|============================================= | 74%
|
|============================================= | 75%
|
|============================================= | 76%
|
|============================================== | 76%
|
|============================================== | 77%
|
|=============================================== | 78%
|
|=============================================== | 79%
|
|================================================ | 79%
|
|================================================ | 80%
|
|================================================ | 81%
|
|================================================= | 81%
|
|================================================= | 82%
|
|================================================== | 83%
|
|================================================== | 84%
|
|=================================================== | 84%
|
|=================================================== | 85%
|
|=================================================== | 86%
|
|==================================================== | 86%
|
|==================================================== | 87%
|
|===================================================== | 88%
|
|===================================================== | 89%
|
|====================================================== | 89%
|
|====================================================== | 90%
|
|====================================================== | 91%
|
|======================================================= | 91%
|
|======================================================= | 92%
|
|======================================================== | 93%
|
|======================================================== | 94%
|
|========================================================= | 94%
|
|========================================================= | 95%
|
|========================================================= | 96%
|
|========================================================== | 96%
|
|========================================================== | 97%
|
|=========================================================== | 98%
|
|=========================================================== | 99%
|
|============================================================| 99%
|
|============================================================| 100%
#>
#> Run completed!
# Summarise it a few different ways
summary(GlenOut) # Default is for quantiles of ages at predictPosition values
#> Quantiles of predicted ages by depth:
#> Depth 2.5% 25% 50% 75% 97.5%
#> 0 -3.000 -1.00 0.0 0.00 1.000
#> 10 10.000 31.00 60.5 137.00 497.075
#> 20 20.000 64.00 119.0 239.25 714.000
#> 30 30.975 97.00 176.0 318.50 827.050
#> 40 43.000 130.00 236.0 405.25 927.100
#> 50 56.925 164.00 296.0 479.00 1010.275
#> 60 68.000 199.75 349.0 539.50 1075.850
#> 70 80.000 236.00 401.0 615.25 1223.125
#> 80 91.975 278.75 441.0 682.50 1267.150
#> 90 105.925 319.00 494.0 734.00 1353.375
#> 100 118.975 364.00 552.0 788.00 1410.100
#> 110 130.975 401.00 603.5 838.25 1488.050
#> 120 148.850 444.50 660.0 897.25 1567.050
#> 130 172.950 488.75 714.5 956.25 1643.025
#> 140 188.950 531.00 769.5 1015.50 1703.325
#> 150 210.925 577.00 826.0 1085.75 1738.025
#> 160 233.000 622.25 872.5 1159.00 1771.075
#> 170 264.675 662.75 922.0 1224.25 1811.275
#> 180 283.925 712.75 966.0 1284.25 1840.050
#> 190 300.925 757.50 1020.5 1329.25 1862.050
#> 200 321.875 803.75 1063.0 1391.25 1930.000
#> 210 344.850 843.00 1119.0 1425.25 1960.225
#> 220 374.000 898.75 1175.0 1469.50 1996.150
#> 230 428.875 935.75 1223.0 1515.25 2042.025
#> 240 478.850 997.75 1277.5 1557.00 2061.050
#> 250 521.825 1041.75 1330.0 1605.00 2077.075
#> 260 555.900 1104.50 1383.5 1664.00 2099.050
#> 270 586.925 1156.50 1447.5 1711.25 2129.100
#> 280 614.775 1213.50 1498.5 1758.00 2154.050
#> 290 682.825 1275.75 1551.5 1805.00 2174.125
#> 300 741.975 1329.00 1602.0 1853.00 2197.025
#> 310 791.725 1382.00 1651.0 1895.00 2222.200
#> 320 825.900 1451.75 1710.5 1935.00 2254.050
#> 330 881.975 1513.50 1761.0 1979.25 2268.075
#> 340 980.400 1569.00 1822.0 2021.00 2284.150
#> 350 1027.975 1629.00 1869.5 2058.25 2310.700
#> 360 1107.950 1693.75 1924.0 2098.00 2352.025
#> 370 1182.925 1753.00 1978.5 2136.25 2369.050
#> 380 1268.000 1828.75 2031.5 2173.00 2421.100
#> 390 1392.875 1902.75 2083.0 2212.00 2459.025
#> 400 1548.225 1995.75 2133.0 2249.00 2508.100
#> 410 1676.750 2078.75 2189.0 2289.25 2551.075
#> 420 1887.925 2168.00 2270.0 2331.00 2607.125
#> 430 2196.975 2323.00 2401.0 2531.00 3139.225
#> 440 2250.975 2413.00 2535.0 2777.00 3657.175
#> 450 2293.975 2489.00 2654.0 2982.25 4009.400
#> 460 2328.975 2557.75 2769.5 3145.25 4249.375
#> 470 2375.950 2627.75 2880.5 3306.25 4605.175
#> 480 2406.950 2704.50 3009.0 3440.50 4779.150
#> 490 2428.975 2783.75 3109.0 3573.25 4917.050
#> 500 2466.000 2852.75 3223.5 3695.25 5088.175
#> 510 2497.000 2927.50 3339.0 3823.50 5263.075
#> 520 2528.975 2994.75 3454.0 3949.50 5429.600
#> 530 2558.975 3081.25 3558.0 4080.00 5660.125
#> 540 2586.950 3155.00 3651.0 4201.75 5817.325
#> 550 2623.000 3239.00 3732.0 4335.50 5973.000
#> 560 2656.825 3315.75 3836.0 4436.25 6128.200
#> 570 2682.950 3397.50 3935.5 4552.50 6268.400
#> 580 2711.925 3492.75 4041.0 4665.25 6411.550
#> 590 2742.800 3577.00 4194.0 4795.00 6572.275
#> 600 2815.850 3648.75 4286.0 4917.75 6670.000
#> 610 2875.500 3742.75 4391.0 5039.75 6767.625
#> 620 2924.750 3843.75 4492.0 5161.00 6896.375
#> 630 2952.925 3925.25 4593.5 5267.00 7084.050
#> 640 3003.500 4013.00 4705.0 5361.50 7139.175
#> 650 3047.675 4116.25 4811.5 5483.25 7193.175
#> 660 3082.950 4216.75 4891.0 5572.00 7264.075
#> 670 3154.625 4311.00 4956.5 5691.25 7349.225
#> 680 3202.850 4395.25 5066.5 5800.25 7411.375
#> 690 3265.850 4480.00 5184.5 5900.00 7452.075
#> 700 3331.425 4562.75 5269.5 5995.25 7512.925
#> 710 3409.750 4685.75 5360.0 6107.25 7703.300
#> 720 3461.900 4794.25 5472.5 6234.25 7772.925
#> 730 3589.025 4885.75 5558.0 6349.25 7884.550
#> 740 3639.675 4995.00 5684.0 6430.25 7976.200
#> 750 3680.975 5101.75 5793.5 6547.00 8041.100
#> 760 3721.975 5211.00 5904.5 6631.75 8183.025
#> 770 3837.125 5292.25 6004.0 6731.25 8287.100
#> 780 3937.725 5377.50 6094.0 6846.50 8368.575
#> 790 3994.700 5478.25 6196.0 6929.00 8420.525
#> 800 4055.325 5582.75 6283.0 7035.00 8482.175
#> 810 4155.875 5677.75 6391.0 7126.25 8631.150
#> 820 4267.375 5773.75 6483.5 7268.50 8691.150
#> 830 4325.350 5877.50 6598.5 7343.00 8781.025
#> 840 4408.725 5979.00 6686.0 7423.75 8852.125
#> 850 4447.600 6126.50 6800.0 7556.50 8887.225
#> 860 4509.975 6218.50 6943.0 7677.50 8915.525
#> 870 4555.800 6302.50 7045.5 7793.25 8988.450
#> 880 4674.300 6389.75 7163.5 7899.25 9048.100
#> 890 4769.700 6484.75 7276.5 8008.00 9112.425
#> 900 4902.025 6576.00 7359.0 8093.25 9179.775
#> 910 4999.275 6675.25 7458.0 8206.75 9222.275
#> 920 5099.750 6807.00 7565.5 8297.25 9311.300
#> 930 5170.900 6899.50 7668.0 8383.50 9461.150
#> 940 5249.275 7007.75 7774.5 8467.25 9508.325
#> 950 5321.700 7116.25 7880.5 8563.75 9600.175
#> 960 5495.775 7240.75 7980.5 8670.25 9665.025
#> 970 5648.975 7374.75 8085.5 8735.00 9707.050
#> 980 5720.250 7503.75 8202.5 8813.00 9752.450
#> 990 5974.800 7632.75 8311.0 8901.25 9798.525
#> 1000 6052.275 7736.00 8420.5 8994.25 9851.375
#> 1010 6221.425 7873.00 8538.0 9089.25 9900.100
#> 1020 6289.525 7992.50 8637.0 9179.75 9931.000
#> 1030 6376.325 8161.75 8755.0 9282.25 9972.650
#> 1040 6524.100 8267.75 8869.0 9370.00 10032.000
#> 1050 6687.975 8417.00 8993.5 9470.00 10065.050
#> 1060 6887.375 8515.50 9104.5 9562.25 10089.050
#> 1070 7097.300 8638.75 9198.5 9628.50 10115.150
#> 1080 7182.175 8761.75 9301.0 9705.25 10148.150
#> 1090 7382.000 8905.75 9411.5 9790.25 10178.075
#> 1100 7535.650 9042.75 9526.0 9870.50 10208.075
#> 1110 7798.925 9183.75 9643.5 9944.00 10246.025
#> 1120 8063.275 9347.25 9757.5 10013.00 10274.075
#> 1130 8358.950 9493.50 9876.0 10082.00 10300.000
#> 1140 8617.825 9689.75 9991.5 10155.00 10340.075
#> 1150 9018.375 9883.75 10108.5 10221.00 10379.025
#> 1160 9483.500 10123.00 10225.0 10299.00 10437.050
#> 1170 10304.975 10376.00 10434.0 10515.00 10828.200
#> 1180 10424.900 10609.00 10669.0 10743.00 11032.175
#> 1190 10543.975 10846.00 10900.0 10962.00 11139.050
#> 1200 10751.975 11086.00 11132.0 11173.00 11279.025
#> 1210 11147.000 11252.00 11300.5 11385.00 11808.100
#> 1220 11209.950 11323.00 11391.0 11541.00 12026.525
#> 1230 11235.975 11382.00 11479.5 11663.25 12157.425
#> 1240 11272.925 11445.75 11568.5 11784.25 12272.125
#> 1250 11300.950 11509.00 11649.0 11880.50 12339.075
#> 1260 11332.875 11585.75 11737.0 11976.25 12405.025
#> 1270 11365.000 11649.75 11829.0 12066.00 12490.025
#> 1280 11415.975 11716.75 11921.0 12151.25 12544.100
#> 1290 11444.975 11793.75 12009.5 12240.25 12594.125
#> 1300 11476.950 11869.00 12096.5 12323.25 12637.075
#> 1310 11523.875 11971.25 12187.0 12387.00 12683.025
#> 1320 11572.950 12060.00 12272.5 12454.00 12727.025
#> 1330 11638.000 12138.50 12354.0 12523.00 12764.000
#> 1340 11743.775 12222.75 12442.0 12586.00 12802.025
#> 1350 11817.625 12324.50 12525.5 12653.00 12837.175
#> 1360 11943.975 12458.75 12620.0 12711.25 12880.050
#> 1370 12132.925 12593.00 12709.0 12777.00 12933.025
#> 1380 12492.650 12750.00 12797.5 12861.00 13009.025
#> 1390 12823.975 12884.00 12937.0 13008.50 13182.400
#> 1400 12884.975 12993.75 13043.0 13120.00 13277.000
#> 1410 12937.950 13101.00 13155.5 13219.00 13349.025
#> 1420 12990.900 13205.75 13265.0 13309.00 13408.000
#> 1430 13148.800 13324.00 13372.5 13415.00 13518.075
#> 1440 13359.975 13451.00 13514.0 13621.00 14532.125
#> 1450 13397.000 13514.00 13627.5 13846.00 14907.475
#> 1460 13421.000 13573.00 13733.0 14049.00 15325.700
#> 1470 13444.925 13635.75 13835.5 14246.25 15547.250
#> 1480 13470.950 13698.75 13943.0 14417.25 15799.400
#> 1490 13494.000 13755.75 14070.5 14599.75 16134.675
#> 1500 13516.000 13812.75 14168.0 14748.50 16286.350
summary(GlenOut, type = "convergence") # Check model convergence
#> Convergence check (watch for too many small p-values):
#> p-value
#> RateMean 0.00000
#> RateVar 0.01176
#> Outlier 4 0.01238
#> Outlier 2 0.05257
#> Outlier 3 0.05579
#> Outlier 6 0.07844
#> Outlier 1 0.11689
#> Top-1 0.11736
#> Beta-100897 0.13802
#> Outlier 5 0.24248
#> Beta-100899 0.25745
#> Beta-100900 0.29266
#> Beta-100901 0.33965
#> Beta-122061 0.36752
summary(GlenOut, type = "outliers") # Look at outlier probabilities
#> Posterior outlier probability by date:
#> Date OutlierProb
#> Top-1 0.013
#> Beta-122061 0.008
#> Beta-100901 0.008
#> Beta-100900 0.009
#> Beta-100899 0.014
#> Beta-100897 0.010
# Predict for some new positions
predictAges <- predict(GlenOut,
newPositions = c(150, 725, 1500),
newPositionThicknesses = c(5, 0, 20)
)
#>
|
| | 0%
|
| | 1%
|
|= | 1%
|
|= | 2%
|
|== | 3%
|
|== | 4%
|
|=== | 4%
|
|=== | 5%
|
|=== | 6%
|
|==== | 6%
|
|==== | 7%
|
|===== | 8%
|
|===== | 9%
|
|====== | 9%
|
|====== | 10%
|
|====== | 11%
|
|======= | 11%
|
|======= | 12%
|
|======== | 13%
|
|======== | 14%
|
|========= | 14%
|
|========= | 15%
|
|========= | 16%
|
|========== | 16%
|
|========== | 17%
|
|=========== | 18%
|
|=========== | 19%
|
|============ | 19%
|
|============ | 20%
|
|============ | 21%
|
|============= | 21%
|
|============= | 22%
|
|============== | 23%
|
|============== | 24%
|
|=============== | 24%
|
|=============== | 25%
|
|=============== | 26%
|
|================ | 26%
|
|================ | 27%
|
|================= | 28%
|
|================= | 29%
|
|================== | 29%
|
|================== | 30%
|
|================== | 31%
|
|=================== | 31%
|
|=================== | 32%
|
|==================== | 33%
|
|==================== | 34%
|
|===================== | 34%
|
|===================== | 35%
|
|===================== | 36%
|
|====================== | 36%
|
|====================== | 37%
|
|======================= | 38%
|
|======================= | 39%
|
|======================== | 39%
|
|======================== | 40%
|
|======================== | 41%
|
|========================= | 41%
|
|========================= | 42%
|
|========================== | 43%
|
|========================== | 44%
|
|=========================== | 44%
|
|=========================== | 45%
|
|=========================== | 46%
|
|============================ | 46%
|
|============================ | 47%
|
|============================= | 48%
|
|============================= | 49%
|
|============================== | 49%
|
|============================== | 50%
|
|============================== | 51%
|
|=============================== | 51%
|
|=============================== | 52%
|
|================================ | 53%
|
|================================ | 54%
|
|================================= | 54%
|
|================================= | 55%
|
|================================= | 56%
|
|================================== | 56%
|
|================================== | 57%
|
|=================================== | 58%
|
|=================================== | 59%
|
|==================================== | 59%
|
|==================================== | 60%
|
|==================================== | 61%
|
|===================================== | 61%
|
|===================================== | 62%
|
|====================================== | 63%
|
|====================================== | 64%
|
|======================================= | 64%
|
|======================================= | 65%
|
|======================================= | 66%
|
|======================================== | 66%
|
|======================================== | 67%
|
|========================================= | 68%
|
|========================================= | 69%
|
|========================================== | 69%
|
|========================================== | 70%
|
|========================================== | 71%
|
|=========================================== | 71%
|
|=========================================== | 72%
|
|============================================ | 73%
|
|============================================ | 74%
|
|============================================= | 74%
|
|============================================= | 75%
|
|============================================= | 76%
|
|============================================== | 76%
|
|============================================== | 77%
|
|=============================================== | 78%
|
|=============================================== | 79%
|
|================================================ | 79%
|
|================================================ | 80%
|
|================================================ | 81%
|
|================================================= | 81%
|
|================================================= | 82%
|
|================================================== | 83%
|
|================================================== | 84%
|
|=================================================== | 84%
|
|=================================================== | 85%
|
|=================================================== | 86%
|
|==================================================== | 86%
|
|==================================================== | 87%
|
|===================================================== | 88%
|
|===================================================== | 89%
|
|====================================================== | 89%
|
|====================================================== | 90%
|
|====================================================== | 91%
|
|======================================================= | 91%
|
|======================================================= | 92%
|
|======================================================== | 93%
|
|======================================================== | 94%
|
|========================================================= | 94%
|
|========================================================= | 95%
|
|========================================================= | 96%
|
|========================================================== | 96%
|
|========================================================== | 97%
|
|=========================================================== | 98%
|
|=========================================================== | 99%
|
|============================================================| 99%
|
|============================================================| 100%
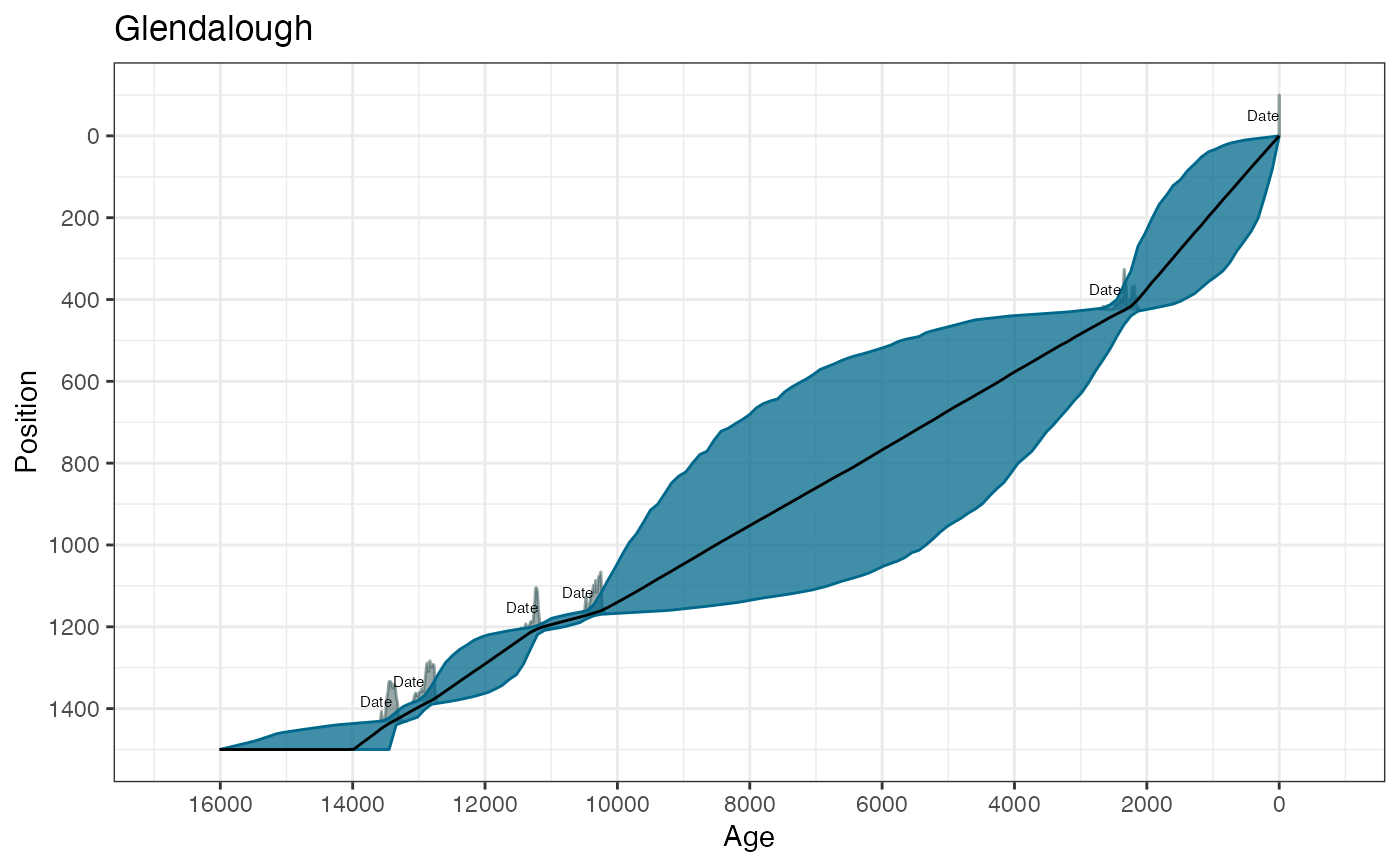
# Plot the output
plot(GlenOut) +
ggplot2::labs(
title = "Glendalough",
xlab = "Age (cal years BP)",
ylab = "Depth (cm)"
)
#> Ignoring unknown labels:
#> • xlab : "Age (cal years BP)"
#> • ylab : "Depth (cm)"
# If you need to specify your own starting values
startingAges <- c(0, 2000, 10000, 11000, 13000, 13500)
GlenOut <- with(
Glendalough,
Bchronology(
ages = ages,
ageSds = ageSds,
calCurves = calCurves,
positions = position,
positionThicknesses = thickness,
ids = id,
predictPositions = seq(0, 1500, by = 10),
thetaStart = startingAges
)
)
#> Running Bchronology...
#>
|
| | 0%
|
| | 1%
|
|= | 1%
|
|= | 2%
|
|== | 3%
|
|== | 4%
|
|=== | 4%
|
|=== | 5%
|
|=== | 6%
|
|==== | 6%
|
|==== | 7%
|
|===== | 8%
|
|===== | 9%
|
|====== | 9%
|
|====== | 10%
|
|====== | 11%
|
|======= | 11%
|
|======= | 12%
|
|======== | 13%
|
|======== | 14%
|
|========= | 14%
|
|========= | 15%
|
|========= | 16%
|
|========== | 16%
|
|========== | 17%
|
|=========== | 18%
|
|=========== | 19%
|
|============ | 19%
|
|============ | 20%
|
|============ | 21%
|
|============= | 21%
|
|============= | 22%
|
|============== | 23%
|
|============== | 24%
|
|=============== | 24%
|
|=============== | 25%
|
|=============== | 26%
|
|================ | 26%
|
|================ | 27%
|
|================= | 28%
|
|================= | 29%
|
|================== | 29%
|
|================== | 30%
|
|================== | 31%
|
|=================== | 31%
|
|=================== | 32%
|
|==================== | 33%
|
|==================== | 34%
|
|===================== | 34%
|
|===================== | 35%
|
|===================== | 36%
|
|====================== | 36%
|
|====================== | 37%
|
|======================= | 38%
|
|======================= | 39%
|
|======================== | 39%
|
|======================== | 40%
|
|======================== | 41%
|
|========================= | 41%
|
|========================= | 42%
|
|========================== | 43%
|
|========================== | 44%
|
|=========================== | 44%
|
|=========================== | 45%
|
|=========================== | 46%
|
|============================ | 46%
|
|============================ | 47%
|
|============================= | 48%
|
|============================= | 49%
|
|============================== | 49%
|
|============================== | 50%
|
|============================== | 51%
|
|=============================== | 51%
|
|=============================== | 52%
|
|================================ | 53%
|
|================================ | 54%
|
|================================= | 54%
|
|================================= | 55%
|
|================================= | 56%
|
|================================== | 56%
|
|================================== | 57%
|
|=================================== | 58%
|
|=================================== | 59%
|
|==================================== | 59%
|
|==================================== | 60%
|
|==================================== | 61%
|
|===================================== | 61%
|
|===================================== | 62%
|
|====================================== | 63%
|
|====================================== | 64%
|
|======================================= | 64%
|
|======================================= | 65%
|
|======================================= | 66%
|
|======================================== | 66%
|
|======================================== | 67%
|
|========================================= | 68%
|
|========================================= | 69%
|
|========================================== | 69%
|
|========================================== | 70%
|
|========================================== | 71%
|
|=========================================== | 71%
|
|=========================================== | 72%
|
|============================================ | 73%
|
|============================================ | 74%
|
|============================================= | 74%
|
|============================================= | 75%
|
|============================================= | 76%
|
|============================================== | 76%
|
|============================================== | 77%
|
|=============================================== | 78%
|
|=============================================== | 79%
|
|================================================ | 79%
|
|================================================ | 80%
|
|================================================ | 81%
|
|================================================= | 81%
|
|================================================= | 82%
|
|================================================== | 83%
|
|================================================== | 84%
|
|=================================================== | 84%
|
|=================================================== | 85%
|
|=================================================== | 86%
|
|==================================================== | 86%
|
|==================================================== | 87%
|
|===================================================== | 88%
|
|===================================================== | 89%
|
|====================================================== | 89%
|
|====================================================== | 90%
|
|====================================================== | 91%
|
|======================================================= | 91%
|
|======================================================= | 92%
|
|======================================================== | 93%
|
|======================================================== | 94%
|
|========================================================= | 94%
|
|========================================================= | 95%
|
|========================================================= | 96%
|
|========================================================== | 96%
|
|========================================================== | 97%
|
|=========================================================== | 98%
|
|=========================================================== | 99%
|
|============================================================| 99%
|
|============================================================| 100%
#>
#> Run completed!
# }